আমরা প্রতিদিন এমন অনেক সমস্যার মুখোমুখি হই, যেগুলো অনুপাত ও সমানুপাতের ধারণা ব্যবহার করে সহজেই সমাধান করা যায়। তাই শিক্ষার্থীদের অনুপাত ও সমানুপাতের ধারণা ও এর প্রয়োগের দক্ষতা অর্জন করা দরকার। একইভাবে, আমাদের দৈনন্দিন জীবনে অনেকখানি জায়গা জুড়ে আছে লেনদেন আর যার সাথে জড়িত লাভ-ক্ষতি। এ কারণে লাভ-ক্ষতি সম্পর্কে শিক্ষার্থীদের পরিষ্কার ধারণা থাকা প্রয়োজন। তাই এ অধ্যায়ে অনুপাত-সমানুপাত ও লাভ-ক্ষতি সম্পর্কিত বিষয় আলোচনা করা হয়েছে ।

অধ্যায় শেষে শিক্ষার্থীরা -

• বহুরাশিক ও ধারাবাহিক অনুপাত ব্যাখ্যা করতে পারবে।
• সমানুপাতের ধারণা ব্যাখ্যা করতে পারবে।
• সমানুপাত সংক্রান্ত সমস্যা সমাধান করতে পারবে।
• লাভ-ক্ষতি কী তা ব্যাখ্যা করতে পারবে।
• লাভ-ক্ষতি সংক্রান্ত সমস্যার সমাধান করতে পারবে।
• কর, ভ্যাট, কমিশন ও মুদ্রাবিনিময় সংক্রান্ত দৈনন্দিন জীবনের সমস্যা সমাধান করতে পারবে।
• ঐকিক ও অনুপাত ব্যবহার করে বাস্তব জীবনে সময় ও কাজ, নল ও চৌবাচ্চা, সময় ও দূরত্ব এবং নৌকা ও স্রোত বিষয়ক সমস্যা সমাধান করতে পারবে।

বহুরাশিক অনুপাত: মনে করি, একটি বাক্সের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে ৮ সে.মি., ৫ সে.মি. ও ৬ সে.মি.
দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত ৮ : ৫ : ৬
সংক্ষেপে, দৈর্ঘ্য: প্রস্থ: উচ্চতা ৮ : ৫ : ৬

এখানে তিনটি রাশির অনুপাত উপস্থাপন করা হয়েছে। এরূপ তিন বা ততোধিক রাশির অনুপাতকে বহুরাশিক অনুপাত বলে।

ধারাবাহিক অনুপাত: মনে করি, পুত্র ও পিতার বয়সের অনুপাত= ১৫ : ৪১ (পূর্ব রাশি: উত্তর রাশি)
এবং পিতা ও দাদার বয়সের অনুপাত= ৪১ : ৬৫

দুটি অনুপাতকে একত্র করে পাই, পুত্রের বয়স পিতার বয়স দাদার বয়স ১৫ : ৪১ : ৬৫। এ ধরনের অনুপাতকে ধারাবাহিক অনুপাত বলে। এখানে লক্ষণীয় যে, প্রথম অনুপাতের উত্তর রাশি ও দ্বিতীয় অনুপাতের পূর্ব রাশি সমান। প্রথম অনুপাতের উত্তর রাশি ও দ্বিতীয় অনুপাতের পূর্ব রাশি সমান না হলে তাদেরকে সমান করে ধারাবাহিক অনুপাত বের করতে হয়।

উদাহরণ ১। ৭ : ৫ এবং ৮ : ৯ দুটি অনুপাত। এদেরকে ধারাবাহিক অনুপাতে প্রকাশ কর।

সমাধান:

১ম অনুপাত = ৭ : ৫

= $\frac{৭}{৫}$

= $\frac{৭\times \overline{)৮}}{৫\times \overline{)৮}}=\frac{৫৬}{৪০}$

= ৫৬ : ৪০

২য় অনুপাত = ৮ : ৯

= $\frac{৮}{৯}$

= $\frac{৮\times \overline{)৫}}{৯\times \overline{)৫}}$

= $\frac{৪০}{৪৫}$

= ৪০ : ৪৫

অনুপাত দুটির ধারাবাহিক অনুপাত ৫৬ : ৪০ : ৪৫

বিকল্প সমাধান

১ম অনুপাত $$\begin{gathered} =৭ : ৫ \\ = ৭\times \overline{)৮} : ৫\times \overline{)৮} \end{gathered}$$

= ৫৬ : ৪০

২য় অনুপাত $$\begin{gathered} = ৮ : ৯ \\ =৮ \times \overline{)৫} : ৯ \times \overline{)৫} \end{gathered}$$

= ৪০ : ৪৫

মনে করি, সোহাগ কোনো দোকান থেকে ১০ টাকা দিয়ে একটি চিপসের প্যাকেট এবং ২৫ টাকা দিয়ে ১ কেজি লবণ কিনল। এখানে লবণ ও চিপস্ এর দামের অনুপাত= ২৫ : ১০ বা ৫ : ২।

আবার, সোহাগদের শ্রেণিতে শিক্ষার্থীর সংখ্যা ৭০। এদের মধ্যে ছাত্র ৫০জন এবং ছাত্রী ২০জন। এখানে ছাত্র ও ছাত্রীসংখ্যার অনুপাত= ৫০ : ২০ বা ৫ : ২। উভয়ক্ষেত্রে অনুপাত দুটি সমান।

অতএব, আমরা বলতে পারি, ২৫ : ১০ = ৫০ : ২০। এই অনুপাতে ৪টি রাশি আছে। এই ৪টি রাশির একটি সমানুপাত তৈরি করেছে।

এর মধ্যে ১ম রাশি ২৫, ২য় রাশি ১০, ৩য় রাশি ৫০ এবং ৪র্থ রাশি ২০ হিসেবে বিবেচনা করলে আমরা লিখতে পারি,

সমানুপাতের ১ম ও ২য় রাশি সমজাতীয় এবং ৩য় ও ৪র্থ রাশি সমজাতীয় হবে।
অর্থাৎ ৪ টি রাশি সমজাতীয় হওয়ার প্রয়োজন নেই। প্রত্যেক অনুপাতের রাশি দুইটি সমজাতীয় হলেই সমানুপাত তৈরি হয়।

সমানুপাতের ১ম ও ৪র্থ রাশিকে প্রান্তীয় রাশি এবং ২য় ও ৩য় রাশিকে মধ্য রাশি বলে। সমানুপাতে '=' চিহ্নের
পরিবর্তে '::' চিহ্নও ব্যবহার করা হয়। অতএব আমরা লিখতে পারি,

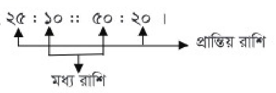
বা, ১ম রাশি/২য় রাশি = ৩য় রাশি/৪র্থ রাশি

বা, ১ম রাশি $\times$ ৪র্থ রাশি = ২য় রাশি $\times$ ৩য় রাশি

ত্রৈরাশিক

আমরা জানি, ১ম রাশি $\times$ ৪র্থ রাশি = ২য় রাশি $\times$ ৩য় রাশি

মনে করি,

১ম, ২য় ও ৩য় রাশি যথাক্রমে ৯, ১৮, ২০।

তবে ৯ $\times$ ৪র্থ রাশি = ১৮ $\times$ ২০

$\therefore$ ৪র্থ রাশি = $\frac{{}^{২}\cancel{১৮} \times ২০ }{\cancel{{৯}_{১}}}= ৪০$

$\therefore$ ৪র্থ রাশি = ৪০

লক্ষ করি

• সমানুপাতের ১ম ও ৪র্থ রাশিকে প্রান্তীয় রাশি বলে।
• সমানুপাতের ২য় ও ৩য় রাশিকে মধ্য রাশি বলে।

উদাহরণ ২। ৩, ৬,৭ এর ৪র্থ সমানুপাতী নির্ণয় কর।

সমাধান : এখানে ১ম রাশি ৩, ২য় রাশি ৬, ৩য় রাশি ৭

আমরা জানি,

১ম রাশি $\times$ ৪র্থ রাশি = ২য় রাশি $\times$ ৩য় রাশি

৩ $\times$ ৪র্থ রাশি = ৬ $\times$ ৭

বা, ৪র্থ রাশি = $\frac{{}^{২}\cancel{৬}\times ৭}{{\cancel{৩}}_{১}}$

বা, ১৪

নির্ণেয় ৪র্থ সমানুপাতিক ১৪

উদাহরণ ৩। ৮, ৭ এবং ১৪ এর ৩য় রাশি নির্ণয় কর।

সমাধান: এখানে ১ম রাশি ৮, ২য় রাশি ৭ এবং ৪র্থ রাশি ১৪

আমরা জানি,

১ম রাশি $\times$ ৪র্থ রাশি = ২য় রাশি $\times$ ৩য় রাশি

বা, ৮ $\times$ ১৪ = ৭ $\times$ ৩য় রাশি

$\therefore$৩য় রাশি = $\frac{৮\times {\cancel{১৪}}^{২}}{\cancel{{৭}_{১}}}$

= ১৬

ক্রমিক সমানুপাত

মনে করি, ৫ টাকা, ১০ টাকা ও ২০ টাকা এই তিনটি রাশি দ্বারা ৫: ১০ এবং ১০: ২০ এই দুটি অনুপাত নেওয়া হলো। এখানে, ৫: ১০: ১০: ২০। এ ধরনের সমানুপাতকে ক্রমিক সমানুপাত বলে। ৫ টাকা, ১০ টাকা ও ২০ টাকাকে ক্রমিক সমানুপাতী বলে।

ক: খ :: খ গ সমানুপাতটির তিনটি রাশি ক, খ, গ ক্রমিক সমানুপাতী হলে $\frac{ক }{খ}=\frac{খ}{গ}$ বাক $\times$ গ = (খ)^২ হবে।

অর্থাৎ, ১ম ও ৩য় রাশির গুণফল দ্বিতীয় রাশির বর্গের সমান।

লক্ষ করি:

• ২য় রাশিকে ১ম ও ৩য় রাশির মধ্য সমানুপাতী বা মধ্য রাশি বলে।
• ক্রমিক সমানুপাতের তিনটি রাশিই সমজাতীয়।

উদাহরণ ৪। একটি ক্রমিক সমানুপাতের ১ম ও ৩য় রাশি যথাক্রমে ৪ ও ১৬ হলে, মধ্য সমানুপাতী ও ক্রমিক সমানুপাত নির্ণয় কর।

সমাধান: আমরা জানি, ১ম রাশি $\times$ ৩য় রাশি = (২য় রাশি)^২

এখানে, ১ম রাশি = ৪ এবং ৩য় রাশি = ১৬

$\therefore$ ৪ $\times$ ১৬ = (মধ্য রাশি)^২

অথবা, (মধ্য রাশি)^২ = ৬৪

মধ্য রাশি = $\sqrt{৬৪}=৮$

নির্ণেয় ক্রমিক সমানুপাত ৪ : ৮ :: ৮ : ১৬ এবং নির্ণেয় মধ্য সমানুপাতী ৮

উদাহরণ ৫। ৫টি খাতার দাম ২০০ টাকা হলে, ৭টি খাতার দাম কত?

সমাধান: এখানে খাতার সংখ্যা বাড়লে দামও বাড়বে।
অর্থাৎ, খাতার সংখ্যার অনুপাত= খাতার দামের অনুপাত

৫ : ৭ = ২০০ টাকা : ৭টি খাতার দাম

বা, $\frac{৫ }{৭}$ = ২০০ টাকা/ ৭টি খাতার দাম

বা, ৭টি খাতার দাম = ৭ $\times$ ২০০ টাকা / ৫ = ২৮০ টাকা।

উদাহরণ ৬। ১২জন লোক একটি কাজ ৯ দিনে করতে পারে। একই হারে কাজ করলে ১৮জনে কাজটি কত দিনে করতে পারবে?

সমাধান: লক্ষ করি, লোকসংখ্যা বাড়লে সময় কম লাগবে, আবার লোকসংখ্যা কমলে সময় বেশি লাগবে। লোকসংখ্যার সরল অনুপাত সময়ের ব্যস্ত অনুপাতের সমান হবে।

১২ : ১৮ = নির্ণেয় সময় : ৯ দিন

বা, $\frac{{}^{২}\cancel{১২}}{\cancel{১{৮}_{৩}}}$= নির্ণেয় সময় / ৯ দিন

বা নির্ণেয় সময় = $\frac{২{\times }^{৩}\cancel{৯} }{\cancel{{৩}_{১}}}$দিন = ৬ দিন

সমানুপাতিক ভাগ

মনে করি, ৫০০ টাকা ৩ : ২ অনুপাতে বণ্টন করতে হবে।

এখানে ৩ : ২ অনুপাতের পূর্বরাশি ও উত্তর রাশির যোগফল = ৩+২ = ৫

১ম ভাগ = ৫০০ টাকার $\frac{৩}{৫}$ অংশ = ৩০০ টাকা

এবং ২য় ভাগ = ৫০০ টাকার $\frac{২}{৫}$ অংশ = ২০০ টাকা।

অতএব,

এভাবে উপরের পদ্ধতিতে একটি রাশিকে বিভিন্ন ভাগে বিভক্ত করা যায়।

উদাহরণ ৭। ২০ মিটার কাপড়কে তিন ভাইবোন অমিত, সুমিত ও চৈতির মধ্যে ৫: ৩ : ২ অনুপাতে ভাগ করলে প্রত্যেকের কাপড়ের পরিমাণ কত?

সমাধান: কাপড়ের পরিমাণ = ২০ মিটার

প্রদত্ত অনুপাত = ৫ : ৩ : ২

অনুপাতের সংখ্যাগুলোর যোগফল = ৫+৩+২ = ১০

অমিতের অংশ = ২০ মিটারের $\frac{৫ }{১০}$অংশ = ১০ মিটার

সুমিতের অংশ = ২০ মিটারের $\frac{৩ }{১০}$ অংশ = ৬ মিটার

এবং চৈতির অংশ = ২০ মিটারের $\frac{২}{১০}$ অংশ = ৪ মিটার

অমিত, সুমিত ও চৈতির কাপড়ের পরিমাণ যথাক্রমে ১০ মিটার, ৬ মিটার ও ৪ মিটার।

উদাহরণ ৮। পনির ও তপনের আয়ের অনুপাত ৪ : ৩। তপন ও রবিনের আয়ের অনুপাত ৫ : ৪। পনিরের আয় ১২০ টাকা হলে, রবিনের আয় কত?

সমাধান: পনির ও তপনের আয়ের অনুপাত ৪ : ৩ = $\frac{৪}{৩}$ = $\frac{৪\times ৫ }{৩\times ৫}$ = $\frac{২০ }{১৫}$= ২০ : ১৫

তপন ও রবিনের আয়ের অনুপাত $\frac{৫}{৪}$ = $\frac{৫\times ৩ }{৪\times ৩}$ = $\frac{১৫ }{১২}$= ১৫ : ১২

পনিরের আয়: তপনের আয় রবিনের আয় = ২০ : ১৫ : ১২

পনিরের আয়: রবিনের আয় = ২০ : ১২

বা, পনিরের আয় / রবিনের আয় = $\frac{২০ }{১২}$

বা, রবিনের আয় = পনিরের আয় $\times$ ১২ / ২০ টাকা

= $\frac{{}^{৬}\cancel{১২০}\times ১২ }{\cancel{২{০}_{১}}}$ টাকা বা ৭২ টাকা।

$\therefore$ রবিনের আয় ৭২ টাকা

১। নিচের রাশিগুলো দিয়ে সমানুপাত লেখ।

(ক) ৩ কেজি, ৫ টাকা, ৬ কেজি, ১০ টাকা
(খ) ৯ বছর, ১০ দিন, ১৮ বছর ও ২০ দিন
(গ) ৭ সে.মি., ১৫ সেকেন্ড, ২৮ সে.মি. ও ১ মিনিট
(ঘ) ১২টি খাতা, ১৫টি পেনসিল, ২০ টাকা ও ২৫ টাকা
(ঙ) ১২৫ জন ছাত্র ও ২৫জন শিক্ষক, ২৫০০ টাকা ও ৫০০ টাকা

২। নিচের ক্রমিক সমানুপাতের প্রান্তীয় রাশি দুটি দেওয়া আছে। সমানুপাত তৈরি কর।

(ক) ৬, ২৪
(খ) ২৫, ৮১
(গ) ১৬, ৪৯
(ঘ) $\frac{৫}{৭},১\frac{২}{৫}$

(ঙ) ১.৫, ১৩.৫।

৩। শূন্যস্থান পূরণ কর।

(ক) ১১ : ২৫ :: $\square$ : ৫০

(খ) ৭ : $\square$ :: ৮ : ৬৪

(গ) ২.৫: ৫.০ :: ৭ : $\square$

(ঘ) $\frac{১}{৩}: \frac{১}{৫}$:: $\square$ : $\frac{৭}{১০}$

(ঙ) $\square$ : ১২.৫ :: ৫ : ২৫

৪। নিচের রাশিগুলোর ৪র্থ সমানুপাতী নির্ণয় কর।

(ক) ৫, ৭, ১০
(খ) ১৫, ২৫, ৩৩
(গ) ১৬, ২৪, ৩২
(ঘ) $৮,৮\frac{১}{২},৪$
(ঙ) ৫, ৪.৫, ৭

৫। ১৫ কেজি চালের দাম ৬০০ টাকা হলে, এরূপ ২৫ কেজি চালের দাম কত?
৬। একটি গার্মেন্টস ফ্যাক্টরিতে দৈনিক ৫৫০টি শার্ট তৈরি হয়। ঐ ফ্যাক্টরিতে একই হারে ১ সপ্তাহে কতটি শার্ট তৈরি হয়?
৭। কবির সাহেবের তিন পুত্রের বয়স যথাক্রমে ৫ বছর, ৭ বছর ও ৯ বছর। তিনি ৪২০০ টাকা তিন পুত্রকে তাদের বয়স অনুপাতে ভাগ করে দিলেন, কে কত টাকা পাবে?
৮। ২১৬০ টাকা রুমি, জেসমিন ও কাকলির মধ্যে ১: ২: ৩ অনুপাতে ভাগ করে দিলে কে কত টাকা পাবে?
৯। কিছু টাকা লাবিব, সামি ও সিয়ামের মধ্যে ৫: ৪: ২ অনুপাতে ভাগ করে দেওয়া হলো। সিয়াম ১৮০ টাকা পেলে লাবিব ও সামি কত টাকা পাবে নির্ণয় কর।

১০। সবুজ, ডালিম ও লিংকন তিন ভাই। তাদের পিতা ৬৩০০ টাকা তাদের মধ্যে ভাগ করে দিলেন। এতে সবুজ ডালিমের $\frac{৩}{৫}$ অংশ এবং ডালিম লিংকনের দ্বিগুণ টাকা পায়। প্রত্যেকের টাকার পরিমাণ বের কর।

১১। তামা, দস্তা ও রূপা মিশিয়ে এক রকমের গহনা তৈরি করা হলো। ঐ গহনায় তামা ও দস্তার অনুপাত ১: ২ এবং দস্তা ও রুপার অনুপাত ৩:৫। ১৯ গ্রাম ওজনের গহনায় কত গ্রাম রূপা আছে?

১২। দুটি সমান মাপের গ্লাস শরবতে পূর্ণ আছে। ঐ শরবতে পানি ও সিরাপের অনুপাত যথাক্রমে প্রথম গ্লাসে ৩ : ২ ও দ্বিতীয় গ্লাসে ৫ : ৪। ঐ দুটি গ্লাসের শরবত একত্রে মিশ্রণ করলে পানি ও সিরাপের অনুপাত নির্ণয় কর।

১৩। কঃ খ = ৪ : ৭, খঃ গ = ১০ : ৭ হলে, ক খ গ নির্ণয় কর।

১৪। ৯৬০০ টাকা সারা, মাইমুনা ও রাইসার মধ্যে ৪ : ৩ : ১ অনুপাতে ভাগ করে দিলে কে কত টাকা পাবে?

১৫। তিনজন ছাত্রের মধ্যে ৪২০০ টাকা তাদের শ্রেণি অনুপাতে ভাগ করে দেওয়া হলো। তারা যদি যথাক্রমে ৬ষ্ঠ, ৭ম ও ৮ম শ্রেণির শিক্ষার্থী হয়, তবে কে কত টাকা পাবে?

১৬। সোলায়মান ও সালমানের আয়ের অনুপাত ৫ ৭। সালমান ও ইউসুফের আয়ের অনুপাত ৪ : ৫। সোলায়মানের আয় ১২০ টাকা হলে ইউসুফের আয় কত?

একজন দোকানদার ১ ডজন বলপেন ৬০ টাকায় ক্রয় করে ৭২ টাকায় বিক্রয় করলেন। এখানে দোকানদার ১২টি বলপেন ৬০ টাকায় ক্রয় করলেন। ফলে ১টি বলপেনের ক্রয়মূল্য $\frac{৬০ }{১২}$ টাকা বা ৫ টাকা। আবার তিনি ১২টি বলপেন ৭২ টাকায় বিক্রয় করলেন। ফলে ১টি বলপেনের বিক্রয়মূল্য $\frac{৭২}{১২}$ টাকা বা ৬ টাকা।

১টি বলপেনের ক্রয়মূল্য ৫ টাকা ও বিক্রয়মূল্য ৬ টাকা।
কোনো জিনিস যে মূল্যে ক্রয় করা হয়, তাকে ক্রয়মূল্য এবং যে মূল্যে বিক্রয় করা হয়, তাকে বিক্রয়মূল্য বলে।
ক্রয়মূল্যের চেয়ে বিক্রয়মূল্য বেশি হলে, লাভ হয়।

লাভ = বিক্রয়মূল্য ক্রয়মূল্য = (৬ টাকা - ৫ টাকা) বা ১ টাকা।
এখানে দোকানদার প্রতিটি বলপেনে ১ টাকা করে লাভ করলেন।

আবার মনে করি, একজন কলাবিক্রেতা ১ হালি কলা ২০ টাকায় ক্রয় করে ১৮ টাকায় বিক্রয় করলেন। ক্রয়মূল্যের চেয়ে বিক্রয়মূল্য কম হলে, ক্ষতি বা লোকসান হয়। ক্ষতি = ক্রয়মূল্য বিক্রয়মূল্য = (২০-১৮) টাকা = ২ টাকা

এখানে কলাবিক্রেতা প্রতি হালিতে ২ টাকা করে ক্ষতি করলেন।

মনে করি, একজন কাপড় ব্যবসায়ী মার্কেটের একটি দোকান ভাড়া নিয়ে ৫ জন কর্মচারী নিয়োগ দিলেন। তিনি দোকানের ভাড়া, কর্মচারীদের বেতন, দোকানের বিদ্যুৎ বিল ও অন্যান্য আনুষঙ্গিক খরচ বহন করেন। এ সকল খরচ তাঁর কাপড়ের ক্রয়মূল্যের সাথে যোগ করা হয়। এই যোগফলকেই মোট খরচ বলে। যদি ঐ কাপড় ব্যবসায়ী মাসে ২,০০,০০০ টাকা ব্যবসায় খাটিয়ে ২,৫০,০০০ টাকায় ঐ কাপড় বিক্রয় করেন, তবে তার (২,৫০,০০০ ২,০০,০০০) টাকা বা ৫০,০০০ টাকা লাভ হবে। আবার যদি মাস শেষে ১,৮০,০০০ টাকার কাপড় বিক্রয় করে থাকেন তাহলে তাঁর (২,০০,০০০ ১,৮০,০০০) টাকা বা ২০,০০০ টাকা ক্ষতি বা লোকসান হবে।

লক্ষ করি:

লাভ = বিক্রয়মূল্য - ক্রয়মূল্য

বা, বিক্রয়মূল্য = ক্রয়মূল্য + লাভ

বা, ক্রয়মূল্য = বিক্রয়মূল্য – লাভ

ক্ষতি = ক্রয়মূল্য - বিক্রয়মূল্য

বা, ক্রয়মূল্য = বিক্রয়মূল্য + ক্ষতি

বা, বিক্রয়মূল্য = ক্রয়মূল্য - ক্ষতি

লাভ বা ক্ষতিকে আমরা শতকরায় প্রকাশ করতে পারি। যেমন, উপরের আলোচনায় ৫ টাকায় বলপেন কিনে ৬ টাকায় বিক্রয় করায় ১ টাকা লাভ হয়।

অর্থাৎ,

৫ টাকায় লাভ হয় ১ টাকা

$\therefore$১ “ ” " $\frac{১}{৫}$ টাকা

$\therefore$১০০ “ ” " $\frac{১\times \cancel{{}^{২০}১০০}}{\cancel{{৫}_{১}}}$ টাকা = ২০ টাকা

$\therefore$ নির্ণেয় লাভ ২০%।

অনুরূপভাবে, কলাবিক্রেতা ২০ টাকার কলা কিনে ১৮ টাকায় বিক্রয় করায় ২ টাকা ক্ষতি হয়েছে।\

অর্থাৎ
২০ টাকায় ক্ষতি হয় ২ টাকা

$\therefore$১ “ ” " $\frac{২}{২০}$ টাকা

$\therefore$১০০ “ ” " $\frac{২\times \cancel{{}^{৫}১০০}}{\cancel{২{০}_{১}}}$ টাকা = ১০ টাকা

$\therefore$নির্ণেয় ক্ষতি ১০%

উদাহরণ ৯। একজন কমলাবিক্রেতা প্রতিশত কমলা ১০০০ টাকায় কিনে ১২০০ টাকায় বিক্রয় করলেন। তাঁর কত লাভ হলো?

সমাধান:

১০০টি কমলার ক্রয়মূল্য ১০০০ টাকা

এবং ১০০টি " বিক্রয়মূল্য ১২০০ "

এখানে ক্রয়মূল্যের চেয়ে বিক্রয়মূল্য বেশি হওয়ায় লাভ হয়েছে।

অর্থাৎ, লাভ = বিক্রয়মূল্য - ক্রয়মূল্য

= ১২০০ টাকা- ১০০০ টাকা

= ২০০ টাকা

নির্ণেয় লাভ ২০০ টাকা।

উদাহরণ ১০। একজন দোকানদার ৫০ কেজির ১ বস্তা চাল ১৬০০ টাকায় কিনলেন। চালের দাম কমে যাওয়ায় ১৫০০ টাকায় বিক্রয় করেন, তাঁর কত ক্ষতি হলো?

সমাধান:

এখানে, ১ বস্তা চালের ক্রয়মূল্য ১৬০০ টাকা

এবং ১ “ ” বিক্রয়মূল্য ১৫০০ টাকা

ক্রয়মূল্যের চেয়ে বিক্রয়মূল্য কম হওয়ায় ক্ষতি হয়েছে।

ক্ষতি = ক্রয়মূল্য বিক্রয়মূল্য

= ১৬০০ টাকা - ১৫০০ টাকা

= ১০০ টাকা

নির্ণেয় ক্ষতি ১০০ টাকা।

উদাহরণ ১১। ৭৫ টাকায় ১৫টি বলপেন কিনে ৯০ টাকায় বিক্রয় করলে শতকরা কত লাভ হবে?

সমাধান:

এখানে, ১৫টি বলপেনের ক্রয়মূল্য ৭৫ টাকা

এবং ১৫টি " বিক্রয়মূল্য ৯০ টাকা

ক্রয়মূল্যের চেয়ে বিক্রয়মূল্য বেশি হওয়ায় লাভ হয়েছে।

$\therefore$লাভ = বিক্রয়মূল্য - ক্রয়মূল্য

= ৯০ টাকা – ৭৫ টাকা

= ১৫ টাকা

$\therefore$৭৫ টাকায় লাভ হয় ১৫ টাকা

১ “ ” " $\frac{১৫}{৭৫}$ টাকা

১০০ “ ” " $\frac{{}^{১}\cancel{১৫}{\times }^{২০}\cancel{১০০}}{\cancel{৭{{৫}_{\cancel{৫}}}_{১}}}$টাকা = ২০ টাকা

অতএব লাভ ২০%।

উদাহরণ ১২। একজন মাছবিক্রেতা প্রতি হালি ইলিশ মাছ ১৬০০ টাকায় কিনে প্রতিটি মাছ ৩৫০ টাকা করে বিক্রয় করলেন। তাঁর শতকরা কত লাভ বা ক্ষতি হলো?

সমাধান:

প্রতি হালি বা ৪টি ইলিশের দাম = ১৬০০ টাকা

১টি “ ” = $\frac{\cancel{{}^{৪০০}১৬০০ }}{\cancel{{৪}_{১}}}$টাকা = ৪০০ টাকা

আবার, ১টি ইলিশের বিক্রয়মূল্য ৩৫০ টাকা

এখানে, ক্রয়মূল্যের চেয়ে বিক্রয়মূল্য কম হওয়ায় ক্ষতি হয়েছে।

ক্ষতি = ক্রয়মূল্য - বিক্রয়মূল্য

= ৪০০ টাকা ৩৫০ টাকা

= ৫০ টাকা

$\therefore$৪০০ টাকায় ক্ষতি হয় ৫০ টাকা

১ “ ” " $\frac{৫০ }{৪০০}$ টাকা

১০০ “ ” " $\frac{{}^{২৫}\cancel{৫০}{\times }^{১}\cancel{১০০}}{\cancel{৪০{{০}_{\cancel{৪}}}_{১}}}$ টাকা বা $\frac{২৫}{২}$ টাকা বা $১২\frac{১}{২}$ টাকা

ক্ষতি $১২\frac{১}{২}$ %

উদাহরণ ১৩। একবাক্স আঙ্গুর ২৭৫০ টাকায় বিক্রয় করায় ৪৫০ টাকা ক্ষতি হলো। ঐ আঙ্গুর ৩৬০০ টাকায় বিক্রয় করলে কত লাভ বা ক্ষতি হতো?

সমাধান:

আঙ্গুরের বিক্রয়মূল্য = ২৭৫০ টাকা

ক্ষতি = ৪৫০ টাকা (যোগ করে)
ক্রয়মূল্য = ৩২০০ টাকা

আবার, বিক্রয়মূল্য = ৩৬০০ টাকা

ক্রয়মূল্য = ৩২০০ টাকা (বিয়োগ করে )

লাভ = ৪০০ টাকা

$\therefore$লাভ ৪০০ টাকা।

উদাহরণ ১৪। একজন চা ব্যবসায়ী একবাক্স চা পাতা কেজি প্রতি ৮০ টাকা হিসাবে ক্রয় করেন। সব চা পাতা কেজি প্রতি ৭৫ টাকা দরে বিক্রয় করায় ৫০০ টাকা ক্ষতি হয়। তিনি কত কেজি চা পাতা ক্রয় করেছিলেন?

সমাধান:

কেজি প্রতি চা পাতার ক্রয়মূল্য ৮০ টাকা

“ ” “ ” বিক্রয়মূল্য ৭৫ টাকা

$\therefore$১ কেজি চা পাতা বিক্রয় করলে ক্ষতি হয় ৫ টাকা

$\therefore$৫ টাকা ক্ষতি হয় ১ কেজিতে

১ “ ” " $\frac{১}{৫}$ কেজিতে

৫০০ “ ” " $\frac{১\times ৫০০}{৫}$কেজিতে

= ১০০ কেজিতে

$\therefore$ চা পাতা ক্রয় করেছিলেন ১০০ কেজি।

উদাহরণ ১৫। একজন ডিম বিক্রেতা প্রতি ডজন ডিম ১০১ টাকা দরে ৫ ডজন এবং ৯০ টাকা দরে ৬ ডজন ডিম কিনে কত দরে বিক্রয় করলে তাঁর ডজন প্রতি ৩ টাকা লাভ হবে?

সমাধান:

১ ডজন ডিমের ক্রয়মূল্য ১০১ টাকা

৫ “ ” " ১০১ $\times$ ৫ টাকা বা ৫০৫ টাকা

আবার, ১ ডজন ডিমের ক্রয়মূল্য ৯০ টাকা

৬ “ ” " ৯০$\times$ ৬ টাকা বা ৫৪০ টাকা

$\therefore$(৫+৬) ডজন বা ১১ ডজন ডিমের ক্রয়মূল্য (৫০৫ + ৫৪০) টাকা বা ১০৪৫ টাকা

১ “ ” " $\frac{১০৪৫ }{১১}$ টাকা বা ৯৫ টাকা

গড়ে ১ ডজন ডিমের ক্রয়মূল্য ৯৫ টকা

ডজন প্রতি ৩ টাকা লাভে ১ ডজন ডিমের বিক্রয়মূল্য (৯৫+৩) টাকা বা ৯৮ টাকা

$\therefore$প্রতি ডজন ডিমের বিক্রয়মূল্য ৯৮ টাকা হলে ডজন প্রতি ৩ টাকা লাভ হবে।

উদাহরণ ১৬। একটি ছাগল ১০% ক্ষতিতে বিক্রয় করা হলো। বিক্রয়মূল্য ৪৫০ টাকা বেশি হলে ৫% লাভ হতো। ছাগলটির ক্রয়মূল্য কত?

সমাধান:

মনে করি, ছাগলটির ক্রয়মূল্য ১০০ টাকা

১০% ক্ষতিতে বিক্রয়মূল্য (১০০ ১০) টাকা বা, ৯০ টাকা
৫% লাভে বিক্রয়মূল্য (১০০+৫) টাকা = ১০৫ টাকা

৫% লাভে বিক্রয়মূল্য - ১০% ক্ষতিতে বিক্রয়মূল্য

বিক্রয়মূল্য ১৫ টাকা বেশি হলে ক্রয়মূল্য
$\therefore$ বিক্রয়মূল্য ১৫ টাকা বেশি হলে ক্রয়মূল্য ১০০ টাকা

১ “ ” “ ” $\frac{১০০ }{১৫}$ টাকা

৪৫০ “ ” “ ” $\frac{১০০ \times { }^{৩০}\cancel{৪৫০ }}{\cancel{১{৫}_{১}}}$ টাকা

= ৩০০০ টাকা

ছাগলটির ক্রয়মূল্য ৩০০০ টাকা

উদাহরণ ১৭। নাবিল মিষ্টির দোকান থেকে প্রতি কেজি ২৫০ টাকা হিসাবে ২ কেজি সন্দেশ ক্রয় করল। ভ্যাটের হার ৪ টাকা হলে, সন্দেশ ক্রয় বাবদ সে দোকানিকে কত টাকা দেবে?

সমাধান:

১ কেজি সন্দেশের দাম ২৫০ টাকা

২ “ ” " $\frac{8 }{১০০}$ টাকা

৫০০ “ ” " $\frac{৪{\times }^{৫}\cancel{৫০০ }}{\cancel{১০{০}_{১}}}$ টাকা = ২০ টাকা

নাবিল সন্দেশ ক্রয় বাবদ দোকানিকে দেবে (৫০০ + ২০) টাকা বা ৫২০ টাকা।

লক্ষণীয়: কোনো দ্রব্যের ক্রয়মূল্যের সাথে নির্দিষ্ট হারে প্রদানকৃত করকে মূল্য সংযোজন কর ভ্যাট (Value Added Tax) বলে।

১। একজন দোকানদার প্রতি মিটার ২০০ টাকা দরে ৫ মিটার কাপড় কিনে প্রতি মিটার ২২৫ টাকা দরে বিক্রয় করলে কত লাভ হয়েছে?

২। একজন কমলাবিক্রেতা প্রতি হালি ৬০ টাকা দরে ৫ ডজন কমলা কিনে প্রতি হালি ৫০ টাকা দরে বিক্রয় করলে কত ক্ষতি হয়েছে?

৩।রবি প্রতি কেজি ৪০ টাকা দরে ৫০ কেজি চাউল কিনে ৪৪ টাকা কেজি দরে বিক্রয় করলে কত লাভবা ক্ষতি হবে?

8।প্রতি লিটার মিল্কভিটা দুধ ৫২ টাকায় কিনে ৫৫ টাকা দরে বিক্রয় করলে শতকরা কত লাভ হয়?

৫।প্রতিটি চকলেট ৮ টাকা হিসেবে ক্রয় করে ৮-৫০ টাকা হিসেবে বিক্রয় করে ২৫ টাকা লাভ হলো, মোট কয়টি চকলেট ক্রয় করা হয়েছিল?

৬।প্রতি মিটার ১২৫ টাকা দরে কাপড় ক্রয় করে ১৫০ টাকা দরে বিক্রয় করলে দোকানদারের ২০০০ টাকা লাভ হয়। দোকানদার মোট কত মিটার কাপড় ক্রয় করেছিলেন?

৭।একটি দ্রব্য ১৯০ টাকায় ক্রয় করে ১৭৫ টাকায় বিক্রয় করলে শতকরা কত লাভ বা ক্ষতি হবে?

৮।২৫ মিটার কাপড় যে মূল্যে ক্রয় করে, সেই মূল্যে ২০ মিটার কাপড় বিক্রয় করলে শতকরা কত লাভবা ক্ষতি হবে?

৯।৫ টাকায় ৮টি আমলকি ক্রয় করে ৫ টাকায় ৬টি দরে বিক্রয় করলে শতকরা কত লাভ বা ক্ষতি হবে?

১০। একটি গাড়ির বিক্রয়মূল্য গাড়িটির ক্রয়মূল্যের $\frac{৪}{৫}$ অংশের সমান। শতকরা লাভ বা ক্ষতি নির্ণয় কর।

১১। একটি দ্রব্য ৪০০ টাকায় বিক্রয় করলে যত ক্ষতি হয় ৪৮০ টাকায় বিক্রয় করলে, তার তিনগুণ লাভ হয়। দ্রব্যটির ক্রয়মূল্য নির্ণয় কর।

১২। একটি ঘড়ি ৬২৫ টাকায় বিক্রয় করলে ১০% ক্ষতি হয়। কত টাকায় বিক্রয় করলে ১০% লাভ হবে?

১৩। মাইশা প্রতি মিটার ২০ টাকা দরে ১৫ মিটার লাল ফিতা ক্রয় করল। ভ্যাটের হার ৪ টাকা। সে দোকানিকে ৫০০ টাকার একটি নোট দিল। দোকনি তাকে কত টাকা ফেরত দেবেন?

১৪। মি. রায় একজন সরকারি কর্মকর্তা। তিনি তীর্থস্থান পরিদর্শনের জন্য ভারতে যাবেন। যদি বাংলাদেশি ১ টাকা সমান ভারতীয় ০.৮৫ রুপি হয়, তবে ভারতীয় ৪২,৫০০ রুপির জন্য বাংলাদেশের কত টাকা প্রয়োজন হবে?

১৫। নীলিম সাহেব একজন চাকরিজীবী। তাঁর মাসিক মূলবেতন ২২,২৫০ টাকা। বার্ষিক মোট আয়ের প্রথম দুই লক্ষ পঞ্চাশ হাজার টাকার আয়কর ০ (শূন্য) টাকা। পরবর্তী টাকার উপর আয়করের হার ১০ টাকা হলে নীলিম কর বাবদ কত টাকা পরিশোধ করেন?

স্থির পানি ও স্রোতস্বিনী নদীতে নৌকার বেগ এক হবে না। স্রোতস্বিনী নদীতে স্রোতের অনুকূলে (একই দিকে) নৌকা চালালে নৌকার নিজস্ব বেগের সাথে স্রোতের বেগ যোগ করতে হবে। স্রোতের প্রতিকূলে (বিপরীত দিকে) নৌকার নিজস্ব বেগ থেকে স্রোতের বেগ বিয়োগ করতে হবে। স্রোতের অনুকূলে বা প্রতিকূলে নৌকা যে গতিতে চলে তা হলো নৌকার কার্যকরী গতিবেগ।

উদাহরণ ২০। একটি নৌকা স্থির পানিতে ঘণ্টায় ৬ কি.মি. যেতে পারে। স্রোতের প্রতিকূলে ৬ কি.মি. যেতে নৌকাটির ৩ গুণ সময় লাগে। স্রোতের অনুকূলে ৫০ কি.মি. যেতে নৌকাটির কত সময় লাগবে?\

সমাধান:

নৌকাটি স্থির পানিতে ৬ কি.মি. যায় ১ ঘণ্টায়

স্রোতের প্রতিকূলে ৬ কি.মি. যায় ১০৩ ঘণ্টায় বা ৩ ঘণ্টায়

প্রশ্নমতে, ৩ ঘণ্টায় যায় ৬ কি.মি.

১ “ ” $\frac{৬}{৩}$ কি.মি. বা ২ কি.মি.

স্রোতের প্রতিকূলে (বিপরীত দিকে) নৌকার কার্যকরী বেগ = নৌকার প্রকৃত বেগ - স্রোতের বেগ

স্রোতের বেগ = নৌকার প্রকৃত বেগ - নৌকার কার্যকরী বেগ

= (৬ - ২) কি.মি. বা ৪ কি.মি. প্রতি ঘণ্টায়

স্রোতের অনুকূলে নৌকার (একই দিকে) কার্যকরী বেগ = নৌকার প্রকৃত গতিবেগ + স্রোতের বেগ

= (৬ + ৪) কি.মি. বা ১০ কি.মি. প্রতি ঘণ্টায়

স্রোতের অনুকূলে ১০ কি.মি. যায় ১ ঘণ্টায়

“ ” ১ “ " $\frac{১}{১০}$ ঘণ্টায়

“ ” ৫০ “ ” $\frac{১{\times }^{৫}\cancel{৫০}}{\cancel{১{০}_{১}}}$ ঘণ্টায় বা ৫ ঘণ্টায়

স্রোতের অনুকূলে যেতে ৫ ঘণ্টা লাগবে।

উদাহরণ ২১। ৬০ মিটার দীর্ঘ একটি ট্রেনের গতিবেগ ঘণ্টায় ৪৮ কি.মি.। রেললাইনের পাশের একটি খুঁটিকে অতিক্রম করতে ট্রেনটির কত সময় লাগবে?

সমাধান:

খুঁটিটি অতিক্রম করতে ট্রেনটিকে নিজের দৈর্ঘ্যের সমান দূরত্ব অতিক্রম করতে হবে।

৪৮ কি.মি. = ৪৮ $\times$ ১০০০ মিটার বা ৪৮০০০ মিটার

ট্রেনটি ৪৮০০০ মি. অতিক্রম করে ১ ঘণ্টায়

“ ১ ” “ ” $\frac{১}{৪৮০০০}$ ঘণ্টায় বা $\frac{১\times ৬০ \times ৬০ }{৪৮০০০}$ সেকেন্ডে

“ ৬০ ” “ ” $\frac{১\times \cancel{৬০}{\times }^{৩}\cancel{৬০}{\times }^{৩}\cancel{৬০}}{{\cancel{৪৮০০০}}_{\cancel{{৪}_{২}}}^{\cancel{৮}}}$ সেকেন্ডে

$=\frac{৯}{২}$ সেকেন্ডে

$=৪\frac{১ }{২}$সেকেন্ডে

ট্রেনটি $=৪\frac{১ }{২}$ সেকেন্ডে খুঁটিটি অতিক্রম করবে।

১। ৪ : ৯ এর দ্বিভাজিত অনুপাত কোনটি?

(ক) ২ : ৩
(খ) ৪ : ৯
(গ) ৯ : ৪
(ঘ) ১৬ : ৮১

২। কঃখ ৪ : ৭ এবং খঃগ=১০ : ৭ হলে গঃখঃক এর মান কত?

(ক) ৪৯ : ৭০ : ৪০
(খ) ৪৯ : ৪০ : ৭০
(গ) ৪০ : ৭০ : ৪৯
(ঘ) ৪০ : ৪৯ : ৭০

৩। ৪ : ৩ ও ৫ : ৬ এর ধারাবাহিক অনুপাতের দ্বিতীয় রাশির মান কত?

(ক) ২০
(খ) ১৮
(গ) ১৬
(ঘ) ১৫

নিচের তথ্যের ভিত্তিতে ৪-৫ নং প্রশ্নের উত্তর দাও।

৩০ মিটার কাপড় মাইশা, মারিয়া ও তানিয়ার মধ্যে ৫ : ৩ : ২ অনুপাতে ভাগ করে দেওয়া হল।

৪। মাইশা কত মিটার কাপড় পেল?

(ক) ১৫
(খ) ৯
(গ) ৬
(ঘ) ৫

৫। তানিয়া থেকে মারিয়া কত মিটার কাপড় বেশি পেল?

(ক) ৩
(খ) ৫
(গ) ৬
(ঘ) ৯

৬। ৫ : ৩ এবং ২ : ৫ এর ধারাবাহিক অনুপাত কোনটি?

(ক) ১০ : ৬ : ১৫
(খ) ৩ : ৫ : ৬
(গ) ৫ : ৬ : ৫
(ঘ) ১৫ : ৬ : ১০

৭। ৩,৫,১৫ এর চতুর্থ সমানুপাতি কোনটি?

(ক) ২০
(খ) ২৫
(গ) ৩০
(ঘ) ৩৫

৮। একজন দোকানদার একটি দিয়াশলাই বাক্স ১.৫০ টাকায় ক্রয় করে ২.০০ টাকায় বিক্রয় করলে তাঁর শতকরা কত লাভ হবে?

ক) ২০%
(খ) ১৫%
(গ) ২৫%
(ঘ) $৩৩\frac{১}{৩}$ %

৯। একজন কলাবিক্রেতা প্রতি হালি কলা ২৫ টাকা দরে ক্রয় করে প্রতি হালি ২৭ টাকা দরে বিক্রয় করলে, তাঁর ৫০ টাকা লাভ হয়। সে কত হালি কলা ক্রয় করেছিল?

(ক) ২৫ হালি
(খ) ২০ হালি
(গ) ৫০ হালি
(ঘ) ২৭ হালি

১০। নিচের রাশিগুলো দাগ টেনে মিল কর।

১১। ৫ জন শ্রমিক ৬ দিনে ৮ বিঘা জমির ফসল উঠাতে পারে। ২০ বিঘা জমির ফসল উঠাতে ২৫ জন শ্রমিকের কত দিন লাগবে?

১২। স্বপন একটি কাজ ২৪ দিনে করতে পারে। রতন উক্ত কাজ ১৬ দিনে করতে পারে। স্বপন ও রতন একত্রে কাজটি কত দিনে শেষ করতে পারবে?

১৩। হাবিবা ও হালিমা একটি কাজ একত্রে ২০ দিনে করতে পারে। হাবিবা ও হালিমা একত্রে ৮ দিন কাজ করার পর হাবিবা চলে গেল। হালিমা বাকি কাজ ২১ দিনে শেষ করল। সম্পূর্ণ কাজটি হালিমা কত দিনে করতে পারত?

১৪। ৩০জন শ্রমিক ২০ দিনে একটি বাড়ি তৈরি করতে পারে। কাজ শুরুর ১০ দিন পরে খারাপ আবহাওয়ার জন্য ৬ দিন কাজ বন্ধ রাখতে হয়েছে। নির্ধারিত সময়ে কাজটি শেষ করতে অতিরিক্ত কতজন শ্রমিক লাগবে?

১৫। একটি কাজ ক ও খ একত্রে ১৬ দিনে, খ ও গ একত্রে ১২ দিনে এবং ক ও গ একত্রে ২০ দিনে করতে পারে। ক, খ ও গ একত্রে কাজটি কত দিনে করতে পারবে?

১৬। একটি চৌবাচ্চায় দুটি নল আছে। প্রথম ও দ্বিতীয় নল দ্বারা যথাক্রমে ১২ ঘণ্টা ও ১৮ ঘণ্টায় খালি চৌবাচ্চাটি পূর্ণ হয়। দুটি নল এক সাথে খুলে দিলে খালি চৌবাচ্চাটি কত ঘণ্টায় পূর্ণ হবে?

১৭ । স্রোতের অনুকূলে একটি নৌকা ৪ ঘণ্টায় ৩৬ কি.মি. পথ অতিক্রম করে। স্রোতের বেগ প্রতিঘণ্টায় ৩ কি.মি. হলে, স্থির পানিতে নৌকার বেগ কত?

১৮। স্রোতের প্রতিকূলে একটি জাহাজ ১১ ঘণ্টায় ৭৭ কি.মি. পথ অতিক্রম করে। স্থির পানিতে জাহাজের গতিবেগ প্রতি ঘণ্টায় ৯ কি.মি. হলে, স্রোতের গতিবেগ প্রতি ঘণ্টায় কত?

১৯। দাঁড় বেয়ে একটি নৌকা স্রোতের অনুকূলে ১৫ মিনিটে ৩ কি.মি. এবং স্রোতের প্রতিকূলে ১৫ মিনিটে ১ কি.মি. পথ অতিক্রম করে। স্থির পানিতে নৌকার গতিবেগ ও স্রোতের পানিতে নৌকার গতিবেগ নির্ণয় কর।

২০। একজন কৃষক ৫ জোড়া গরু দ্বারা ৮ দিনে ৪০ হেক্টর জমি চাষ করতে পারেন। তিনি ৭ জোড়া গরু দ্বারা ১২ দিনে কত হেক্টর জমি চাষ করতে পারবেন?

২১ । লিলি একা একটি কাজ ১০ ঘণ্টায় করতে পারেন। মিলি একা ঐ কাজটি ৮ ঘণ্টায় করতে পারেন। লিলি ও মিলি একত্রে ঐ কাজটি কত ঘণ্টায় করতে পারবেন?

২২। দুটি নল দ্বারা একটি খালি চৌবাচ্চা যথাক্রমে ২০ মিনিটে ও ৩০ মিনিটে পানি-পূর্ণ করা যায়। চৌবাচ্চাটি খালি থাকা অবস্থায় দুটি নল এক সাথে খুলে দেওয়া হলো। প্রথম নলটি কখন বন্ধ করলে চৌবাচ্চাটি ১৮ মিনিটে পানি-পূর্ণ হবে?

২৩। ১০০ মিটার দীর্ঘ একটি ট্রেনের গতিবেগ ঘণ্টায় ৪৮ কিলোমিটার। ঐ ট্রেনটি ৩০ সেকেন্ডে একটি সেতু অতিক্রম করে। সেতুটির দৈর্ঘ্য কত?

২৪। ১২০ মিটার দীর্ঘ একটি ট্রেন ৩৩০ মিটার দীর্ঘ একটি সেতু অতিক্রম করবে। ট্রেনটির গতিবেগ ঘণ্টায় ৩০ কি.মি. হলে, সেতুটি অতিক্রম করতে ট্রেনটির কত সময় লাগবে?

২৫। তামা, দস্তা ও রূপা মিশিয়ে একটি গহনা তৈরি করা হলো। ঐ গহনায় তামা ও দস্তার অনুপাত ১:২ এবং দস্তা: রুপার অনুপাত ৩:৫। গহনার ওজন ১৯০ গ্রাম।
(ক) তামা, দস্তা ও রুপার অনুপাত নির্ণয় কর।
(খ) গহনায় তামা, দস্তা ও রুপার ওজন পৃথকভাবে নির্ণয় কর।
(গ) ঐ গহনায় কি পরিমাণ দস্তা মিশালে তামা ও দস্তার অনুপাত ১:৩ হবে।

২৬। রাসেল একজন ঘড়ি ব্যবসায়ী। তিনি একটি ঘড়ি ৬২৫ টাকায় বিক্রয় করায় ১০% ক্ষতি হলো।

(ক) ঘড়িটি বিক্রিতে কত টাকা ক্ষতি হলো।
(খ) ঘড়িটির ক্রয়মূল্য কত?
(গ) ঘড়িটি কত টাকায় বিক্রয় করলে ১০% লাভ হবে।